2026 Författare: Leah Sherlock | sherlock@quilt-patterns.com. Senast ändrad: 2025-01-24 21:19:38
Förmågan att korrekt visa olika former på arkets plan, duken och vilken annan yta som helst är en ganska betydande färdighet. Och framför allt är det viktigt både för konstmänniskor: målare, skulptörer, grafiker, designers (av interiöra utrymmen och den arkitektoniska miljön), och för vetenskapsmän: matematiker, fysiker, designers, uppfinnare.
Men det är också viktigt för en person som är långt ifrån dessa sfärer att lära sig hur man korrekt uppfattar och visar världen omkring sig. Detta hjälper till att förstå all dess mångsidighet mycket djupare. Om du inte har en tillräcklig uppfattning om hur du gör detta korrekt, kommer du med största sannolikhet inte att lyckas med ett projekt, en bild eller ritning av någon uppfinning. Det vill säga, denna färdighet är viktig både för att lösa enkla, vardagliga uppgifter och för de som har en global, universell betydelse.
Lite historia
Sedan urminnes tider har människor försökt avbilda vad de såg omkring sig: andra människor, några primitiva byggnader från den tiden, en fantastiskt vacker värld av växter och djur, majestätiska berg och helt enkelt saker, husgeråd. Det vill säga världen i all dess mångfald och storhet.
Men då hade de fortfarande ingen aning om hur det kunde göras exakt och kompetent, så att visningen av olika tredimensionella objekt på ett plan var riktigt realistisk, levande. Personen hade inte de relevanta kunskaperna och dessutom fanns det inga speciella färdigheter, förutom kanske för de mest elementära.
Det sägs i tidigare källor att den första målningen i världen bestod av bara en linje som gick längs skuggan av en person som kastades av solen på väggen. Det vill säga, naturen själv föreslog i vilken riktning det är värt att gå på jakt efter den rätta lösningen på denna fråga.
Och denna fråga oroade dåtidens man också av denna anledning: han ville inte bara beundra den omfattande levande siluetten, originalet så att säga, utan försökte fånga ett rumsligt objekt på ett plan. Och han gjorde detta så att han på detta sätt antingen kunde dekorera sitt hem eller en plats som var helig för honom, eller ta med sig en bunt med en bild och flytta den till valfritt avstånd.
Mönstergeometri
Och vad du än säger, men åren gick, århundraden gick, och på något sätt, allt eftersom civilisationen utvecklades, lärde sig människor gradvis att visa komplexa figurer i tvådimensionell rymd, det vill säga på ett plan. Först nu började noggrannheten i storlekarna och proportionerna för de avbildade föremålen verka väldigt ungefärliga.
Men frågan om hur korrekt visningen av figuren på planet och hur mycket de motsvarar volymen på de ursprungliga föremålen, blev en gång mycket relevant. På något sätt kallade en ny vetenskapgeometri. Mer exakt är dess avsnitt beskrivande geometri.
Här studerar hon bara former och plan, linjer och punkter, samt deras förhållande till varandra - både i tredimensionellt och tvådimensionellt rum.
Konverteringsmetoder
En viktig egenskap inom bildkonsten är visningen av figurer på bildplanet. När allt kommer omkring är detta faktiskt fångsten av tredimensionella rumsliga objekt i tvådimensionalitet. Nämligen: komplexet måste omvandlas till ett enkelt, det vill säga ett föremål som har en längd, bredd, höjd måste överföras till ett plan.
Och beskrivande geometri gör sådana "övergångar" tack vare vissa metoder. Det är ungefär sex av dem tot alt. Här är de tre viktigaste och de mest populära runt om i världen:
- perspektiv (när det avbildade objektet tas bort i rymden);
- ortogonal projektion (projektion parallellt, där strålarna är vinkelräta mot planet);
- sned projektion (projektion parallellt, där strålarna lutar i förhållande till planet).
Det avbildade objektet framträder ganska tydligt i axonometrisk projektion (som inkluderar ortogonal och sned). Men det projiceras tydligast och sannast när det visas i perspektiv. Och det är ovanstående metoder som till stor del löser frågan om hur man visar figurer på ett plan.

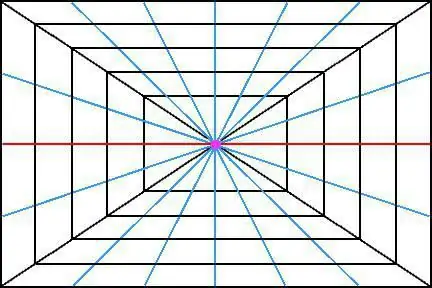
Perspektiv
Perspective tar den mest hedervärda platsen bland andra bildmetoder. Eftersom det mänskliga ögatsom en kameralins ser den det omgivande rummet på ett liknande sätt. Saker som är längre bort från betraktaren verkar mindre i storlek, och ibland mycket mindre, än när de är nära.
Ta till exempel bilden av en kub i rymden. Om, i själva verket, alla dess kanter är parallella med varandra, då när du tittar på detta objekt på avstånd, kan det verka som att kanterna konvergerar (eller borde konvergera) vid en punkt. Och det som är mest intressant, de bör inte bara konvergera vid en punkt, utan ha en enda skärningspunkt.

Tack vare renässansens mästare: Albrecht Dürer, Piero Della Francesca, Andrea Mantegna, Leon Batista Alberti, modern måleri vet vad direkt linjärt perspektiv är, hur man bestämmer höjden på horisonten och försvinnande punkter.
Och det världsberömda geniet - Leonardo da Vinci - argumenterade först för konceptet flygperspektiv. Detta inkluderar en förändring av färgen, ton hos objektet, förändringar i dess kontrastegenskaper (minskar när objektet flyttas bort).

Ortografisk projektion
Ortogonal kallas parallell projektion, som är riktad mot en rät linje, som är vinkelrät mot planet. Under applikationsprocessen förblir dimensionerna på objektets konturer oförändrade. Det vill säga att objektet visas utan förvrängning.
Det projicerade tredimensionella objektet är så att säga uppdelat i tre vyer: från sidan, framifrån och uppifrån. Och tittar på allt detta samtidigt, kan du lägga tillen representation av hur ett föremål ser ut i volym. Samtidigt förblir dimensionerna på figuren oförändrade både i den tredimensionella bilden och i den tvådimensionella.

Sned projektion
Denna projektion är uppdelad i flera underarter, nämligen:
- isometrisk vy;
- dimetrisk projektion;
- trimetrisk projektion.
Isometrisk har distorsionskoefficienter i alla 3 axlarna (längd, bredd, höjd). Det vill säga, vinklarna mellan parvis tagna axlar är lika med 120 grader. I den dimetriska är förvrängningarna längs de två axlarna lika, och den tredje är olika. Och i den trimetriska projektionen är alla distorsionskoefficienter (det vill säga längs alla tre axlarna) olika.
Vridningsformer
När en rätvinklig triangel roterar längs axeln på ett av de två benen, kommer dess tredje sida (hypotenus) att beskriva en ny figur som kallas en kon. Och om du roterar en rektangel (fyrkant) längs en av dess sidor får du en cylinder. När halvcirkeln roterar kommer en sfär att komma ut.
Det följer att genom att rotera planet längs någon axel får vi de så kallade rotationssiffrorna.

Dessa figurer har en rotationsaxel. Hur de ser ut i planet beror på deras placering i förhållande till ögonhöjd. Till exempel är de övre och nedre sidorna av en cylinder i huvudsak cirklar. Och om du tittar på dem i ett plan ser de ut som ellipser.
Men uppgiften blir ännu svårare när den visasrumsliga figurer på planet, de har en lutande axel. Det är viktigt att konturerna av revolutionskropparna är på samma avstånd från den senares axel.
Lite om chiaroscuro
Chiaroscuro spelar en viktig roll för att visa figurer på ett plan. Eftersom volymen av det avbildade objektet skapas inte bara på grund av linjer, utan också på grund av den korrekta fördelningen av ljus och skugga på dess sidor. Och så ser det ganska voluminöst ut i planet för en tvådimensionell yta.

Därmed är visningen av figurer på planet, bestämning av deras storlekar, funktionerna i den korrekta överlagringen av ljushet och mörka fläckar mycket möjliga tack vare ovanstående metoder. Och, viktigast av allt, det är verkligen beprövade metoder i praktiken, som används av vår tids ledande experter.
Rekommenderad:
Jugendstil i arkitektur, måleri och interiör. Hur visar jugend sig i ornament, catering eller dekorationer?

Släta linjer, mystiska mönster och naturliga nyanser - så här kan du karakterisera jugendstilen som fängslade hela Europa i slutet av artonhundratalet och början av 1900-talet. Huvudidén med denna riktning är harmoni med naturen. Det blev så populärt att det täckte alla kreativa specialiteter
Är ett vad ett vad eller ett vad?

Betting är ett argument. Det ingås mellan de tvistande parterna om uppfyllandet av ett visst villkor. I en tvist kan du förlora eller vinna, medan förloraren kommer att uppfylla vinnarens krav, överenskomna i förväg. Vinnaren är den vars tillstånd är sant. När satsar du pengar?
Skräck om djur: från ett husdjur till ett ondskefullt monster - ett slag

Sedan urminnes tider undvek människan vilda djur, mötet med sådana varelser orsakade honom omedveten rädsla. Naturligtvis kunde denna egenskap hos det mänskliga psyket inte låta bli att dra fördel av regissörerna för skräckfilmer. De studerade mästerligt alla typer av zoofobi och började churna fram filmer med läskiga historier baserade på våra vanligaste skräckhistorier från barndomen
Vad är ett kapital? Detta är ett fragment av arkitektur med ett hundraårigt förflutet
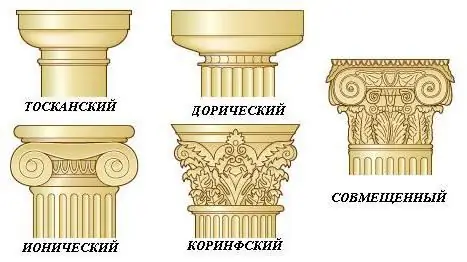
Huvudstaden är idén till stor arkitektur som har kommit till oss från urminnes tider. Vad är ett kapital, varför skapades det och vad är dess roll i vårt moderna liv? Allt detta - i vår lilla artikel
Donjon är ett ointagligt torn inne i ett slott. Donjon i ett medeltida slott, historia, internt arrangemang

Forntida slott är fortfarande fantastiska. Inte ens århundraden av krig och belägringar har raserat deras murar med marken. Och den säkraste platsen för varje slott, dess hjärta, var donjonen - detta är det mest befästa inre tornet. Från den här artikeln kommer du att lära dig vad en donjon är i ett medeltida slott, hur den var ordnad inuti och var dess namn kom ifrån